
Зміст
- Закон Зіпфа пояснив
- Базовий експеримент
- Закон Zipf на ринку Steam
- Що ми можемо дізнатися про Steam?
- Висновки
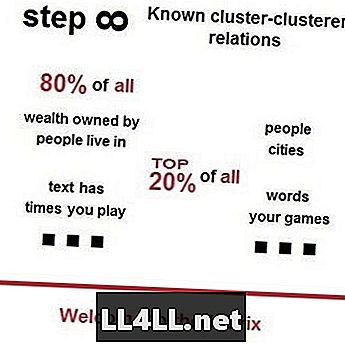
Невдовзі мій друг запропонував мені подивитися відео Vsauces на закон Ципфа, принцип Парето і їх таємничі виступи навколо нас. Ось невеликий тизер, щоб привернути вашу увагу - 80% всіх людей живуть у 20% найпопулярніших міст; 80% всієї землі належить 20% найбагатших поміщиків; 80% всього сміття знаходиться на 20% найстрашніших вулицях, як і передбачено законом Зіпфа і принципом Парето.
Недостатньо? Ну, як я вчора виявив, кроляча діра не зупиняється на цьому ... Повний скептицизму, я вирішив подивитися, скільки часу люди проводять, граючи в Steam ігри ... Ну. 80% часу людей витрачається на 20% найпопулярніших ігор ... Цікаво? Ну, читайте далі, є ще до цієї історії.
Тач у 20min, Vsauces прагнення є awesome та роз'яснює дуже багато великої речовини малюнку про Zipf, але він є дуже сором'язливий у показуючи нам основний механізм що широко вважається щоб сприяти чому Zipf працює як йому. Тому, перш ніж ми продовжимо, я хотів би коротко пояснити це.
Закон Зіпфа пояснив
Існує кілька концептуальних способів пояснити інтуїцію за принципом 20/80. Кращим прикладом, на мою думку, є той, що стосується кратерів Місяця.
Базовий експеримент
Отже, уявіть, якщо ви хочете, що є незаймана Місяць - ідеально гладка поверхня. Тепер, скажімо, є деякі випадково астероїди, які потрапляють на Місяць волею-неволею. Коли перший астероїд приземляється, він залишає кратер. Тепер ще один потрапляє, залишаючи кратер в іншому місці. Кожен кратер є частиною загальної площі поверхні, тому існує ймовірність, що наступний випадковий астероїд вдарить близько до існуючого кратера і з'єднається з ним, утворюючи групу. Ймовірність того, що новий астероїд потрапить у цей кратер, пропорційна існуючим розмірам кратерів і астероїдів. Це означає, що наступний випадковий астероїд, швидше за все, приєднається до найбільшої існуючої групи, що робить її ще більшою. Своєрідний кумулятивний процес, який потім створює багатий-отримати-багатший бідний-get-lonelier механізм.
Майте це на увазі, тому що це вважається загальним поясненням "чому" закон Zipfs працює з такою загадковою універсальністю. Приклад астероїда досить простий, проте питання полягає в тому, що відбудеться через багато повторів
Трохи здивування?
Добре, я зробив gif щоб загнати цей вихідний пункт додому. NB! Графік буде обговорюватися пізніше, просто спробуйте і уявіть експеримент.

Якщо ми спостерігаємо фактичний місяць, то виявляється, що при збільшенні кількості астероїдів до великих кількостей спостерігаються такі діаметри кратерів, що 20% найбільших кратерів наближаються до 80% всієї площі поверхні.
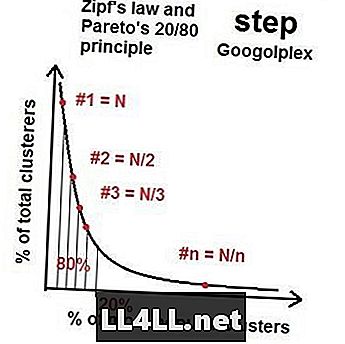
Тому, коли ми переходимо до більшої кількості астероїдів, розподіл найбільш популярних і найменш популярних груп наближається до свого роду "ідеального розподілу" з цим властивістю 20/80 - розподілом Парето. Якщо ви робите математику, виявляється, що (у загальному випадку), якщо найбільша група має розмір N, то друга найбільша група знаходиться навколо розміру N / 2, третій N / 3 і так далі і так далі. Це називається законом Зіпфа. Дивно, що Закон Зіпфа і розподіл Парето працюють над дивовижною кількістю елементів (астероїдів) і груп (кластери кратерів). Звичайно, існують перекоси і випадкові збурення, але загальна тенденція незаперечна.
Я сподіваюся, ви бачите, як астероїди, швидше за все, потрапляють у великі кратери на Місяці, пов'язують міста з привабливішими містами, якщо в них вже живе більше людей. Проте, треба розуміти, що міста далекі від єдиних "груп", які ведуть себе відповідно до Зіпфа.
Ось кілька прикладів з дослідження Марка Ньюманса щодо розподілів Парето. NB! Графіки знаходяться в логарифмічному масштабі, який згладжує гіперболічну форму кривих, що представляє майже лінійне відношення.
Початковий y = aX ^ (- b)
Журнали обох сторін => log y = log a - b log X
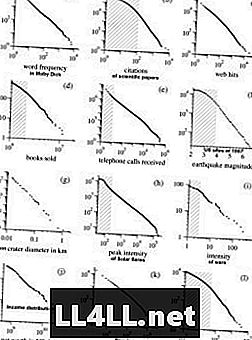
Цікаво, що таку ж тенденцію демонструють і релігійні культи ... Спільна властивість більшості цих явищ - це просто тенденція "великих груп-отримати-більшу". Тому закон Зіпфа зберігається в механізмах, де переваги елементів позитивно пов'язані з розміром груп (тобто, чим більше група, тим більше ймовірність її зростання). Ось чому мені подобається думати про групи як про кластери та елементи як про кластери.
Закон Zipf на ринку Steam
Підозрілий з цього останнього? Ось кількість часу, який люди витрачають на найпопулярніші ігри на Steam .. Дані з SteamSpy.
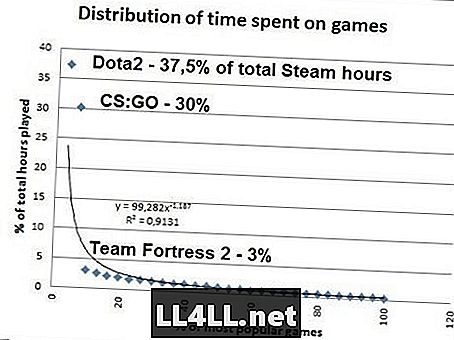
Якщо ви робите математику, виявляється, що 20% найбільш популярних ігор Steam припадають на 80% від загального обсягу гри, тому таємниця Pareto 20/80 працює як шарм ... Тут треба помітити, що для Zipf, щоб бути правдою, CS: GO потребує 37,5% / 2 = 18,8% від загального часу замість колосальних 30%. Але осторонь від цього викид (STOP PLAYING CS: GO), розподіл, подібний до Zipf, явно існує.
Ось кількість проданих копій для найпопулярніших ігор.
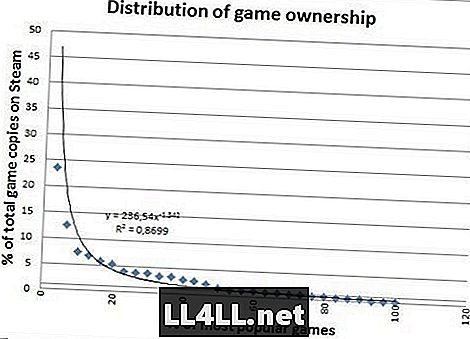
Виглядає набагато краще, а? Копії, що продаються, не мають великих викидів, тому вона дуже добре вписується, що є помітною різницею. Проте з відмінностей двох останніх графіків можна зробити щось більш цікаве.
Ви помічаєте, як "хвіст", що йде вправо, - це вид жиру на другому графіку? Ну, простими словами, це говорить нам, що "відносно непопулярні" ігри насправді є набагато більш популярними, ніж у попередньому сюжеті.
Насправді виявляється, що 20% найбільш популярних ігор припадає лише на 60% продажів, проти 80% гри. Цікаво? Ви ставите свою дупу це.
Що ми можемо дізнатися про Steam?
Щоправда, той факт, що популярність гри випливає з розподілу Парето, говорить нам, що дійсно є якийсь позитивний ефект мережі, який змушує гравців вибирати ігри, які вже грають більше людей. Що різниця у вгодованості хвостів говорить нам, що користувачі Steam є набагато більш "сліпими за розміром групи", коли купують ігри, ніж вони є, коли вони грають.
Подумайте про це - чим більше людей купують ігри, незалежно від "нинішньої популярної думки", тим більше вирівнюється розподіл у Парето, оскільки менш велика ймовірність подальшого зростання великих ігор. Якщо б ніхто не давав щурам приклад про те, скільки людей вже грають в гру, а наявність всіх ігор була однаковою, то ми очікуємо, що 20% найпопулярніших ігор становитимуть близько 50% продажів і часу відтворення (наприклад, якщо прийняти індивідуальні переваги нормально розподілені).
Висновки
Таким чином, існує два фактори, які сприяють розповсюдженню Pareto на ринках Steam - наскільки новаторськими є розробники (скільки нових кратерів Місяця формуються) і скільки геймерів (астероїдів) оцінюють поточний розмір групи, вибираючи, до якої групи . Як виявилося, геймери дуже сліпим для групи при купівлі ігор, але навпаки, коли вони грають їх. Прохолодно?
Якщо ви хочете дізнатися більше про дистрибуції Закону та енергетичного закону Ципфа, тут приємна лекція. Крім того, обов'язково погляньте на папір Ньюмана!
Якщо ви хочете прочитати більше такого роду матеріалу, досить скоро я постараюся приєднати це спостереження до моделі, яка показує, що більш популярні багатокористувацькі ігри мають більш високі ціни (які посилаються на переваги геймерів приєднуватися до груп більшого розміру). Див. Статтю тут. У статті Piece De Resistance з'являться спроби об'єднати ці теорії, пояснюючи, як багатокористувацькі ігри, соціальні мережі та міста є насправді всіма анти-конкуруючими товарами з мережевими ефектами (чим більше людей споживають добро, тим більше переваги для кожного споживача), які мають озаглавив їх цим містером ...
До тих пір - насолоджуйтеся!
P.S. Поп-коментар з цікавою ідеєю для 20/80 відносини, яку ви вважаєте правдою.
Шахта:
80% ностальгії людей спричинені 20% найщасливіших спогадів (фактично перевірених за те, що люди забувають інформацію)
80% маси зосереджено в 20% найбільших космічних об'єктів (фактично доведено для розподілу сили тяжіння)
І звичайно
80% безладу в вашому туалеті припадає на 20% того, що ви їсте (немає академічних досліджень)